Sawtooth wave. Algorithm

Processing Coding Questions
1

Hello Misters and misses,
I need to control a sawtooth wave, like explained wikipedia https://en.wikipedia.org/wiki/Sawtooth_wave
This a kind of triangular wave in wikipedia. You 'll find it here: algorithm in JavaScript
I would like to be able to control the period and the amplitude of the sawtooth wave.
I think, it shouldn’t be very hard to make.

I thank you very much for this work.
Happy new year!

3

Here’s the mathematical solution to this, which should be your main concern:

In Processing, this would look like the following:

float amp = 100;
float period = 80;

void setup() {
  size(600, 600);
}

void draw() {
  background(0);
  
  translate(0, height/2);
  
  stroke(255, 170, 20);
  noFill();
  beginShape();
  
  for (int x=0; x<width; x++) {
    vertex(x, amp*(1-4*abs(((float)x/period+0.5) % 1 - 0.5)));
  }
  
  endShape();
}

I hope this could help you.
Best, Simon

2 Likes
4

Depending on what you’re using the triangle wave for, there’s a few different ways to create them. You can get a pure triangle wave, or you can build a more natural one using sine waves. For both you’ll need:

  • Sample Rate: how many slices per second. Usually audio is at a minimum 44100 samples per second.
  • Phase: wrapped value from 0 to 1 to keep track of the position of the wave in time
  • Frequency: frequency of the waveshape
  • Phase Delta: How much the phase changes each increment of the sample rate (freq / sampleRate)
  • A Phasor: Similar to a Sawtooth Oscillator, except it’s only positive, tracking the phase from 0 to 1.

Draw the Triangle
(pseudocode)

   float sampleRate = 44100.0f;   // Hz
   float phase = 0.0f;
   float freq = 440.0f;   // Hz
   float phaseDelta = freq / sampleRate;  // Amount to increment phase each sample 

   // for each sample occurring at sampleRate, or
   // continuously at sample rate, whichever suits your needs
   phase += phaseDelta;
   
   // Wrap phase
   if (phase > 1.0f)
      phase -= 1.0f;

This should make the Phasor: A ramp from 0 to 1 with the wavelength of your frequency. It starts at zero, and at 1 it is at the end of the cycle and wraps back to zero.

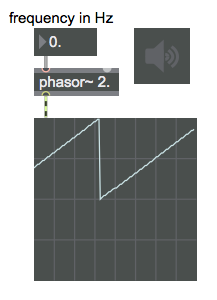
If we offset this by -0.5, we have a sawtooth wave that goes from -0.5 to 0.5
Multiplying by 2 will normalize between -1 and 1
To make that Saw into a Triangle, take the absolute value. All the negative values get “folded up” and it makes a triangle. But it’s all in the positive, so offset it again by -0.5 to get it from -0.5 to 0.5, and multiply by 2 to normalize between -1 and 1

   // Step by step
   float makeSaw = phase - 0.5f;
   float normalizeSaw = makeSaw * 2.0f;
   float makeTraingle = fabsf(normalizeSaw);
   float offsetTriangle = makeTriangle - 0.5f;
   float normalizeTriangle = offsetTriangle * 2.0f;

OR

   // All in one
   float outputValue = ( fabsf( 2 * (phase - 0.5f) ) - 0.5f ) * 2.0f;

The other option, to build a triangle wave by adding multiple sine waves together. Building waves using sine waves is considered more natural sounding, or less harsh, because we can limit the harmonic content, avoiding really harsh high frequencies.

To make a Sine wave is relatively easy. Just find the sine function of the phase time two pi

   float sineSample = sin(phase * TWO_PI);

Now start adding sine waves up the harmonic series for that frequency. For a triangle wave, you’re only using the odd harmonics. Ever alternating harmonic is multiplied by -1. Then the amplitude of each harmonic is scaled by 1 / n^2

the harmonic series is:

fundamental = 1
2nd harmonic = 2/1
3rd harmonic= 3/2
4th harmonic= 4/3
5th harmonic = 5/4
etc...

That just keeps going up forever, so you choose where to stop. For the triangle it would be

 // harmonic  = (freq * ratio) * scale
fundamental = (freq * 1) * ( 1 / 1^2)
3rdHarmonic = (freq * 3/2) * (1 / 3^2) * -1
5thHarmonic = (freq * 5/4) * (1 / 5^2)
7thHarmonic = (freq * 7/6) * (1 / 7^2) * -1
etc...

Either way, you now have a Triangle Wave between -1 and 1. So to control the amplitude, just multiply all the samples by your gain factor.

1 Like