How to create Minimum bounding shapes such as ellipse, triangle, quadrilateral from a given 2d shape

Processing Coding Questions
1

I have a 2d shape(boundary) and generated the convex hull. Now, I want to create a minimum bounding quadrilateral, minimum bounding triangle, and minimum bounding ellipse for that boundary. I have generated these minimum bounding shapes using a predefined function in matlab. But I want to do the same in Processing or C. Any ideas on how to proceed after creating a convex hull for a given 2d shape in C or processing.

2

You have a convex hull?

Check the vertixes in a for loop

For your rect: the smallest x and y = upper left corner, the biggest = lower right corner

3

Bounding rectangle and ellipse are implemented here (in a geometry library Iā€™m close to releasing):

@Chrisir Your suggestion would compute the envelope of the shape, not necessarily the minimum bounding rectangle.

1 Like
4

@Chrisir Thanks for the suggestion. But, this just creates a bounding box. I want to know how to generate these minimum bounding shapes.

2 Likes
5

@micycle Great work! Iā€™m able to generate a minbounding rect and circle. But I want to know how to generate minbounding quadrilateral triangle and ellipse

6

Hi @Goodman,

Searching for ā€œminimum enclosing triangleā€ on Google yields interesting results:

Considering the OBR (Oriented Bounding Rectangle) mentioned by @micycle is a quadrilateral already my guess is that you are looking either for a bounding irregular quadrilateral or for the minimum enclosing parallelogram.
Considering the apparent lack of ready-made function for both, I would suggest to implement your own solution based on the few papers available on the subject (ex: Smallest Enclosing Parallelogram of a Convex Polygon)

7

Funny youā€™ve linked to OpenCV ā€“ I tried porting their C++ implementation to Java the other day.

Sometimes it works:

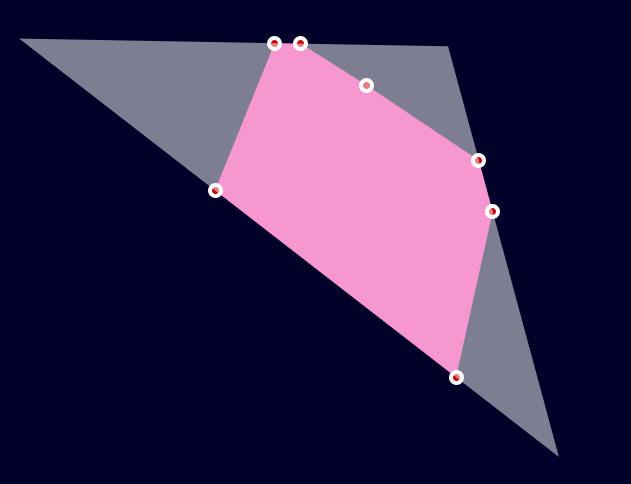
image
image667Ɨ691 13.7 KB
image
image593Ɨ580 13.1 KB
image

Occasionally it doesnā€™t:

image
image871Ɨ724 18.8 KB

Other times thereā€™s no output at all:

image

There might be just one bug in there somewhereā€¦ Anyway, I didnā€™t realise it had a Java interface so Iā€™ll try that and compareā€¦

8

I just ported the algorithm in Python mode based on an implementation I found on GitHub and it seems Iā€™m running into the same kind of issue: it works in most cases but sometimes fails to return a triangle (at all).

Not sure what could be the cause of this but I found out that a slight change in the floating numbers (be it a distance or a vector) usually solves the problem. For instance, calling sqrt from Python ā€˜mathā€™ module sometimes makes possible to return a valid triangle when Processing built-in sqrt function fails to do so. Same thing for PVectors and Python tuples, sometimes one makes the whole thing work when the other doesnā€™t.

For now Iā€™m adding a simple rule at the end of the procedure and it works great so far:

  • if no valid triangle is found ā†’ flip the the order of the input vertices and compute again
    • if still no valid triangle ā†’ add a slight change in the input vertices (Ā± 1x10^-3)

MET
MET1425Ɨ708 107 KB

Here are some polygons (coordinates of convex hulls) that were problematic (without the procedure), if you want to test out:

hull = [PVector(155.12383, 248.58586, 0.0), PVector(161.0123, 179.3106, 0.0), PVector(168.83984, 130.08127, 0.0),  PVector(248.66309, 119.282684, 0.0), PVector(461.89334, 137.37393, 0.0), PVector(475.26022, 199.19283, 0.0),  PVector(245.58762, 380.92023, 0.0)]
    
hull = [PVector(110.02104, 279.57806, 0.0), PVector(123.71097, 101.68562, 0.0), PVector(334.75125, 123.85287, 0.0),  PVector(357.30774, 305.98468, 0.0), PVector(333.9188, 368.8738, 0.0), PVector(303.62317, 390.05, 0.0), PVector(210.75824, 340.84155, 0.0)]
    
hull = [PVector(192.95053, 342.0016, 0.0), PVector(218.2282, 214.57556, 0.0), PVector(356.4301, 116.1142, 0.0), PVector(458.212, 231.65149, 0.0), PVector(429.22546, 332.95416, 0.0), PVector(390.15195, 342.7939, 0.0), PVector(263.15396, 347.68643, 0.0)]
    
hull = [PVector(129.48656, 388.42194, 0.0), PVector(181.31583, 230.62254, 0.0), PVector(212.38477, 167.97357, 0.0), PVector(469.0845, 162.51602, 0.0 ), PVector(486.59265, 234.31108, 0.0), PVector(477.97174, 363.26276, 0.0), PVector(431.43225, 382.64935, 0.0)]
    
hull = [PVector(202.1734, 128.25597, 0.0), PVector(425.54095, 139.74759, 0.0), PVector(428.87698, 295.7047, 0.0), PVector(255.63092, 373.27747, 0.0)]
    
hull = [PVector(128.32523, 105.98023, 0.0), PVector(393.61334, 184.44684, 0.0), PVector(493.83255, 221.63284, 0.0), PVector(411.80234, 359.64954, 0.0), PVector(231.17766, 248.42395, 0.0)]
    
hull = [PVector(110.02104, 279.57806, 0.0), PVector(123.71097, 101.68562, 0.0), PVector(334.75125, 123.85287, 0.0), PVector(357.30774, 305.98468, 0.0), PVector(333.9188, 368.8738, 0.0), PVector(303.62317, 390.05, 0.0),  PVector(210.75824, 340.84155, 0.0)]
    
hull = [PVector(117.05237, 112.30546, 0.0), PVector(393.43924, 145.73712, 0.0), PVector(404.43298, 160.94029, 0.0),  PVector(443.2803, 341.7787, 0.0), PVector(129.86247, 331.0315, 0.0), PVector(117.686295, 218.09064, 0.0)]
    
hull = [PVector(179.54169, 370.20096), PVector(184.75476, 138.93231), PVector(206.79596, 130.36479), PVector(350.9182, 143.59122), PVector(497.7497, 301.03436), PVector(253.6199, 396.03775)]
2 Likes
9

Processing Geometry Suite now has a robust Minimum Bounding Triangle method (first Java implementation as far as I can tell).

ezgif.com-gif-maker (2)

1 Like