Connecting outermost dots with a single line?

Processing Libraries
1

Hi all -

Does anyone know how to work with a way to connect the outermost randomly placed dots to make a shape?

E.g., if you make 25 random points on screen and there are 10 dots on the perimeter and 15 on the inside, I would like to connect the 10 outermost dots with a single line, defining the outline of the “shape”?

Any help is appreciated.
Thanks.

1 Like
2

https://en.wikibooks.org/wiki/Algorithm_Implementation/Geometry/Convex_hull/Monotone_chain
here i play with it:
Andrew's monotone chain algorithm ,

better
Path around a perimeter ,

1 Like
3

Hey -

Thank you for your quick reply. It’s fascinating how many things people are researching these days … I am now wondering if there’s a tool built for Processing that automates many of these processes? Do you know about that?

I know, for instance, that for Grasshopper (add-on) for Rhino 3D, there’s theses plugins that does the trick for you …

Thanks.

1 Like
4

you mean a library, for this i did not know, so i just copy the code into a processing test
yes, might be,
but if it uses a other name for that functionality, how you find it?

i think testing and describing all internal and external libraries
add the java ones you just can load as a .jar
might fill a book.

5

The term of art for that is “convex hull” – and there are several tools that do it: the Mesh library, and openCV (I believe), and you can also just implement the algorithm directly.

http://leebyron.com/mesh/

A Convex Hull is the encompassing shape around a group of points. As if you were to wrap a piece of string around all of the points. This is handy when doing collision tests on complex shapes, or finding the most extreme points within a dataset.

hull

and

For a recent related discussion see:

1 Like
6

Though Andrew’s Monotonous Chain was interesting, so i tried to implement a version using angles yesterday, but got stuck on the chains backtracking. Got lucky today and now it works like a charm :sweat_smile:

So it should be relatively easy to implement it, if you follow the original (also because there‘s Java Code for it in the Wikipedia Page).

7

There is also a Java example of Monotone Chain here:

https://en.wikibooks.org/wiki/Algorithm_Implementation/Geometry/Convex_hull/Monotone_chain#Java

which has an animation demonstrating the search method

…and a video demo of atduskgreg’s hull implementation which also shows the search method:

2 Likes
8

There‘s also a complete Java Code for it there :wink:

9

Hi @clausneergaard,

Adding to the previous suggestions and replying to your question:

  • the Mesh library (already mentioned) has a Hull() class (example) – 2D only
  • the Hemesh library has a HEC_ConvexHull() class (example) – 3D only
  • the ComputationalGeometry library has QuickHull3D() class (example) – 3D only
  • the bRigid libray has BConvexHull() class (example) – 3D only
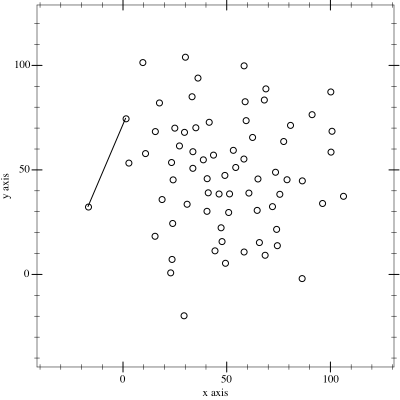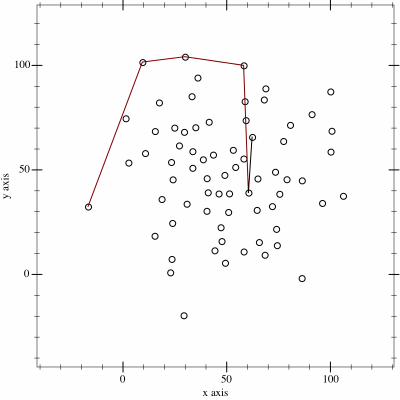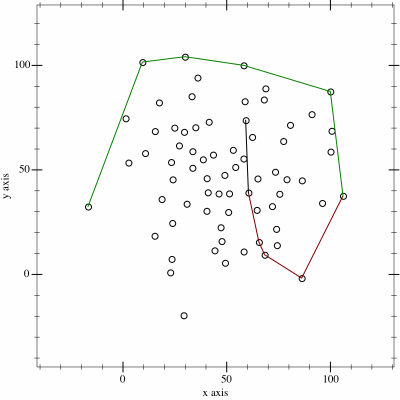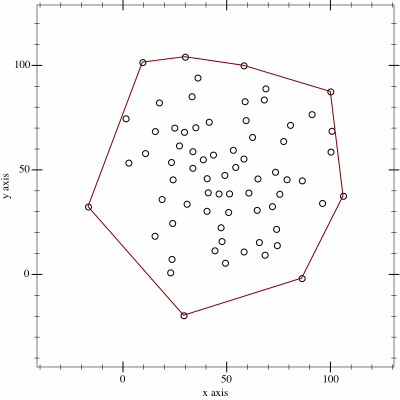
  • the giCentre Utils library has a ConvexHull() class (example below) – 2D only
####Check full documentation here --> http://gicentre.org/utils/reference/

add_library('gicentreUtils')

N = 70
A = 60
points = []

def setup():
    size(1000, 600, P2D)
    background(255)
    strokeWeight(5)
    randomSeed(6)
    smooth(8)
    
    #Display points
    for i in xrange(1, N + 1):
        theta = radians(270 / float(N)) * int(random(N))
        x = width/2 + cos(theta) * random(100, 200)
        y = height/2 + sin(theta) * random(100, 200)
        points.append(PVector(x, y))
        
    #Compute convex Hull
    hull = ConvexHull(points).getHull()
        
    #Draw convex hull edges
    strokeWeight(2)
    stroke(0)
    for i in xrange(len(hull)):
        v1 = hull[i]
        v2 = hull[(i+1)%len(hull)]
        line(v1.x, v1.y, v2.x, v2.y)
        
    #Draw points
    strokeWeight(5)
    stroke(66, 9, 195)
    for p in points:
        point(p.x, p.y)

That being said, if you are trying to make a shape out of a disparate / irregularly distributed 2d point cloud chances are that you are actually looking for a concave hull algorithm (not convex). In that case, I would suggest to use the alphaTriangulate2D() and getAlphaEdges() methods from the Hemesh library.

Example sketch (Python mode):

add_library('hemesh')

N = 70
A = 60
points = []

def setup():
    size(1000, 600, P2D)
    background(255)
    smooth(8)
    
    #Display points
    for i in xrange(1, N + 1):
        theta = radians(270 / float(N)) * int(random(N))
        x = width/2 + cos(theta) * random(100, 200)
        y = height/2 + sin(theta) * random(100, 200)
        points.append(WB_Point(x, y))
        
    #Compute alpha-triangulation
    triangulation = WB_Triangulate2D().alphaTriangulate2D(points)
    
    #Get alpha edges
    alphaEdges = triangulation.getAlphaEdges(A)
    tuplesA = zip(alphaEdges[::2], alphaEdges[1::2])
    
    
    #Draw Points
    stroke(66, 9, 195)
    strokeWeight(5)
    for p in points:
        point(p.x, p.y)
       
    #Draw Contours (alpha edges) 
    stroke(0)
    strokeWeight(2)
    for n, (i1, i2) in enumerate(tuplesA):
        p1 = points[i1]
        p2 = points[i2]
        line(p1.x, p1.y, p2.x, p2.y)

convaxconcave
convaxconcave1087×570 148 KB

Convex Hull with the giCentreUtils library (left) and Concave Hull with the Hemesh library (right)

5 Likes
10

Hello all -

Thanks for all your very interesting replies - I will definitely try out your suggestions. There’s a lot of good info, to get me going, thank you!

Best, Claus