Trig question, drawing an arrow head on an arc

[ddownn]

How can I define points t1 and t2 by their angle from point a, relative to the tangent of the arc?

I would like to draw lines from point a up to line cb by specifying an angle such as 30 or 45 degrees relative to the arc’s tangent at point a.

Here I have hard coded points on line cb a distance of 20 from point b. But I don’t have the math skills to do this based on an angle.

I can do it with pushMatrix and translating/rotating but I’m trying to learn the math. Actually, I’m not even sure how to draw a tangent of an arc without pushMatrix.

PVector c, a, b;
float d;
float r;
int n = 5;
float theta= TWO_PI/n;
float start = theta/2;
float end = start*0.75;
void setup() {
   size(400,600);
   d = 300;
   r = d/2;
   c = new PVector(width/2, height/2);
   a = new PVector(c.x+cos(start)*r, c.y+sin(start)*r);
   b = new PVector(c.x+cos(end)*r, c.y+sin(end)*r);
}
void draw() {
   background(127);
   ellipseMode(RADIUS);

   noFill();
   stroke(0);
   strokeWeight(1);
   arc(c.x, c.y, r, r, 0, theta);
   
   strokeWeight(3);
   stroke(0,200,0);
   arc(c.x, c.y, r, r, 0, start);
   
   strokeWeight(3);
   stroke(0,200,0);
   
   PVector t1 = new PVector(c.x+cos(end)*(r-20), c.y+sin(end)*(r-20));
   
   PVector tail1 = PVector.lerp(a, t1, 1);
   line(a.x, a.y, tail1.x, tail1.y);
   
   PVector t2 = new PVector(c.x+cos(end)*(r+20), c.y+sin(end)*(r+20));
   
   PVector tail2 = PVector.lerp(a, t2, 1);
   line(a.x, a.y, tail2.x, tail2.y);
   
   strokeWeight(1);
   stroke(75);
   line(c.x, c.y, a.x, a.y);
   line(c.x, c.y, b.x, b.y);
   line(b.x, b.y, c.x+cos(end)*(r+50), c.y+sin(end)*(r+50));
}

[William3954]

Preface: not that great at math either.

Using some old functions I made, came close but still off. Here is what I have:

//Put into your draw function
   float ArrowDegrees = 45;
   float ArrowDist = 100;
   PVector ArrowPoint1 = PolarToCart(a, findAngle(b,a)-ArrowDegrees, ArrowDist);
   PVector ArrowPoint2 = PolarToCart(a, findAngle(b,a)+ArrowDegrees, ArrowDist);
   line(a.x,a.y,ArrowPoint1.x,ArrowPoint1.y);
   line(a.x,a.y,ArrowPoint2.x,ArrowPoint2.y);

The following two functions are what wrote awhile ago. Add them after your draw function.

PVector PolarToCart(PVector CenterPointIn, float degreesIn, float radiusIn ) {
  float tx2 = radiusIn*cos(radians(degreesIn));
  float ty2 = radiusIn*sin(radians(degreesIn));
  tx2=tx2+CenterPointIn.x;
  ty2=ty2+CenterPointIn.y;
  return new PVector(tx2, ty2);
}

float findAngle(PVector p0, PVector p1) {
  float a = atan2(p0.y-p1.y, p0.x-p1.x);
  return degrees(a);
}

I think the issue is that I am only grabbing the perpendicular point of BC, not the tangent.

Also, since you are using PVectors, a little trick I like is this function (not used above):

void line(PVector StartPoint, PVector EndPoint) {
  line(StartPoint.x, StartPoint.y, EndPoint.x, EndPoint.y);
}

This way you can just write:

line(a,b);

Hope I was able to help.

[quark]

@ddownn

I can do it with pushMatrix and translating/rotating but I’m trying to learn the math. Actually, I’m not even sure how to draw a tangent of an arc without pushMatrix.

The sketch code below shows the maths needed to create the arc arrow using trigonometry only. The code is commented but if you have questions please ask.
If you run the sketch you will see this

Creating an arrowhead on an arc

PVector centre, p;
float w, h;
float start, end, p_ang, tan_ang, delta;

void setup() {
  size(360, 240);
  centre = new PVector(width/2, height/2);
  w = width * 0.4;
  h = height * 0.35;
  // Set the limits of the arc 
  // start angle must be less than end angle
  start = radians(32);
  end = radians(314);
  // Use these to animate the arc
  p_ang = start;
  delta = radians(0.5);
}

void draw() {
  background(0);
  strokeWeight(2);
  stroke(255);
  noFill();
  // Increment the point angle every frame until we reach the ned
  if (p_ang < end) {
    p_ang += delta;
  }
  // DRaw the current arc
  arc(centre.x, centre.y, 2 * w, 2 * h, start, p_ang);
  p = arcPoint(centre, w, h, p_ang);
  // Approximate the tangent at current point
  PVector tangent = PVector.sub(arcPoint(centre, w, h, p_ang + delta), 
    arcPoint(centre, w, h, p_ang - delta));
  // Calculate the tangent angle
  tan_ang = atan2(tangent.y, tangent.x);
  // Calculate arrow end points relative to the arrow tip
  PVector p0 = rotatePoint(-10, -4, tan_ang);
  PVector p1 = rotatePoint(-10, 4, tan_ang);
  // Draw the arrow sides
  line(p.x, p.y, p.x + p0.x, p.y + p0.y);
  line(p.x, p.y, p.x + p1.x, p.y + p1.y);
}

PVector arcPoint(PVector centre, float aw, float ah, float aa) {
  return new PVector(aw * cos(aa) + centre.x, ah * sin(aa) + centre.y);
}

PVector rotatePoint(float x, float y, float angle) {
  float nx = x * cos(angle) - y * sin(angle);
  float ny = x * sin(angle) + y * cos(angle);
  return new PVector(nx, ny);
}

void keyTyped() {
  // Reset the animation back to the begining if the 's'
  // key is typed
  if (key == 's') {
    p_ang = start;
  }
}

[ddownn]

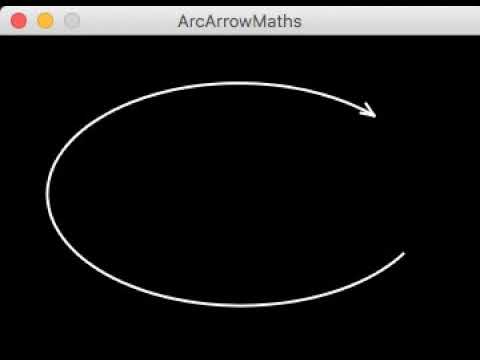
What I am trying for is how to get rid of “magicNumber”, by setting a pair of PVectors at the points where the arrow intersects with the yellow trimLine, no matter how “wide” the arrow head is (in a range that makes sense like 10deg to 60deg), or what the trimAngle is in relation to the startAngle (within a scaleFactor range of about 0.2 and 0.9.)

I used a bit of matrix transforms here to show more closely what I’m trying to do, but I would prefer to understand how to use math to locate A) the tangent line and B) the “trim” points so I can just draw the arrow lines between two PVectors without having to do matrix transforms.

I would like to be able to start at a PVector which here is startPoint, and draw the arrow lines at variable angles in relation to the arc’s tangent at startPoint, i.e. tangent +/-15deg, +/-45deg, +/-60deg, etc, (in this example I used PI/6) up to the points where they would intersect trimLine, without having to do a matrix translate/ rotate.

PVector c;
Arrow a1, a2;
float magicNumber = 50;
void setup() {
  size(400, 600);
  c = new PVector(width/2, height/2);
  a1 = new Arrow(new PVector(c.x, c.y-150), 1, 2.25, 0.95);
  a2 = new Arrow(new PVector(c.x, c.y+150), 32, 3, 0.3);
}
void draw() {
  background(127);
  ellipseMode(RADIUS);

  a1.show(); // a very long arc, the arrow needs a larger trim angle
  a2.show(); // a very short arc, the arrow needs a smaller trim angle
}
class Arrow {
  PVector loc, startPoint, trimLine;
  int n;
  float d, r, theta, startAngle, trimAngle, arrowArcOffset, arrowScaleFactor;
  Arrow(PVector loc, int n, float arrowArcOffset, float arrowScaleFactor) {
    this.loc = loc;
    d = 250;
    r = d/2;
    this.n = n;

    // the arc length will change to fractions of a circle 
    // based on the number of divisions
    theta = TWO_PI/n;

    // startAngle is where the arrow point is, 
    // the offset keeps it closer to the beginning of the arc 
    // to make room for another arrow
    // at the end of the arc which will 
    // point in the opposite direction
    startAngle = theta/arrowArcOffset;

    // trimAngle is the angle where the arrow head 
    // lines should be trimmed to, 
    // arrowScaleFactor will vary so that 
    // the arrow head looks normal 
    // whether the arc length is long or very short
    trimAngle = startAngle*arrowScaleFactor;
    startPoint = new PVector(loc.x+cos(startAngle)*r, loc.y+sin(startAngle)*r);
    trimLine = new PVector(loc.x+cos(trimAngle)*r, loc.y+sin(trimAngle)*r);
  }
  void show() {
    drawCircle();
    drawArc();
    drawStartLine();
    drawArrowArc();
    drawTangent();
    drawArrow();
    drawTrimLine();
  }
  void drawCircle() {
    noFill();
    stroke(200);
    strokeWeight(5);
    ellipse(loc.x, loc.y, r, r);
  }
  void drawArc() {
    noFill();
    stroke(200, 0, 0);
    strokeWeight(1);
    arc(loc.x, loc.y, r, r, 0, theta);
  }
  void drawArrowArc() {
    strokeWeight(2);
    stroke(0, 200, 0);
    arc(loc.x, loc.y, r, r, 0, startAngle);
  }
  void drawStartLine() {
    strokeWeight(1);
    stroke(50);
    line(loc.x, loc.y, startPoint.x, startPoint.y);
  }
  void drawTrimLine() {
    strokeWeight(1);
    stroke(225, 225, 0);
    line(loc.x, loc.y, trimLine.x, trimLine.y);
    line(trimLine.x, trimLine.y, loc.x+cos(trimAngle)*(r+50), loc.y+sin(trimAngle)*(r+50));
  }
  void drawTangent() {
    strokeWeight(1);
    stroke(50);

    pushMatrix();
    translate(startPoint.x, startPoint.y);
    rotate(startAngle-HALF_PI);
    line(0, 0, 200, 0);
    popMatrix();
  }
  void drawArrow() {
    strokeWeight(2);
    stroke(0, 200, 0);

    pushMatrix();
    translate(startPoint.x, startPoint.y);

    pushMatrix();
    rotate(startAngle-HALF_PI-PI/6); // startAngle-HALF_PI is tangent
    line(0, 0, magicNumber, 0);
    popMatrix();

    pushMatrix();
    rotate(startAngle-HALF_PI+PI/6); // startAngle-HALF_PI is tangent
    line(0, 0, magicNumber, 0);
    popMatrix();

    popMatrix();
  }
}

[ddownn]

Thank you for this, I will need a little time to see how it works. I can see tan_ang and rotatePoint() are definitely going to help get a lot closer. It’s the 10 and 4 in your example that I originally set out to solve so I don’t need to hard code the values for the arrow head, so they can be variable length and angle.

[quark]

Solving the 10 and the 4 is simple enough.

Add two new global variables

float arrow_len = 10;          // the length of the arrow arm
float arrow_ang = radians(60); // the angle between the arms

then in draw change the arrow head draw lines to

  // Calculate arrow end points relative to the arrow tip
  float dx = arrow_len * cos(arrow_ang /2); 
  float dy = arrow_len * sin(arrow_ang /2); 
  PVector p0 = rotatePoint(-dx, -dy, tan_ang);
  PVector p1 = rotatePoint(-dx, dy, tan_ang);

Now changing the arrow arm length and included angle can be set programmatically.

[ddownn]

But it’s still a constant value… what if we want the arrow lines’ length to be determined by going right up to intersect with the yellow line in my second example, even as the angle between the arrow start point and the yellow line varies, so that angle will drive the length of the arrow head?

[quark]

@ddownn

But it’s still a constant value

It is only a constant value because I am not varying the values stored in arrow_len and arrow_ang there is no reason why you can’t change these values programmatically based on what you are trying to achieve.

Unfortunately I am not sure what you are trying to do. Perhaps you include a drawing of what you are hoping to achieve.

[humayung]

do you mean the point intersection between two line? so you just grab a line from any point to the intersection point?

intersection between two lines
refer: https://en.wikipedia.org/wiki/Line–line_intersection

So in the code, it will be like this

Point intersect(Line i) {
    float x1 = a.x;
    float x2 = b.x;
    float x3 = i.a.x;
    float x4 = i.b.x;

    float y1 = a.y;
    float y2 = b.y;
    float y3 = i.a.y;
    float y4 = i.b.y;

    float numeratorX = (x1*y2 - y1*x2)*(x3 - x4)-(x1 - x2)*(x3*y4 - y3*x4);
    float numeratorY = (x1*y2 - y1*x2)*(y3 - y4)-(y1 - y2)*(x3*y4 - y3*x4);
    float denumerator = (x1 - x2)*(y3 - y4) - (y1 - y2) * (x3 - x4);

    float px = numeratorX/denumerator;
    float py = numeratorY/denumerator;
    return new Point(px, py);
  }

And
is this kind of thing you want to achieve?

//Mouse Wheel to change angle
Line tail1;
Line tail2;
Line line;
float lineAngle = 0;

float a = 90;
float tailWide = radians(a); // Angle between tails
float arrowRotation = radians(10); // arrow rotation
void setup() {
  size(640, 360);
  noFill();
  tail1 = new Line(arrowRotation + tailWide/2, 0, 0);
  tail2 = new Line(arrowRotation - tailWide/2, 0, 0);
  line = new Line(lineAngle, 100, 100);
}

void draw() {
  background(51);
  translate(width/2, height/2);
  line.set(lineAngle, mouseX - width/2, mouseY - height/2);
  line.draw();
  
  Point p1 = tail1.intersect(line);
  Point p2 = tail2.intersect(line);
  p1.draw();
  p2.draw();
  stroke(255);
  line(p1.x, p1.y, 0, 0);
  line(p2.x, p2.y, 0, 0);
}

void mouseWheel(MouseEvent e){
  lineAngle += e.getCount() * 0.05;
}

class Line {
  PVector a;
  PVector b;
  float slope;
  color color_ = color(random(100, 256), random(100, 256), random(100, 256));
  
  Line(float angle, float driftX, float driftY){
    a = new PVector(cos(angle) * -width + driftX, sin(angle) * -width + driftY);
    b = new PVector(cos(angle) * width + driftX, sin(angle) * width + driftY);
    slope = (a.x - b.x)/(a.y - b.y);
  }

  void draw() {
    stroke(color_);
    line(a.x, a.y, b.x, b.y);
  }

  Point intersect(Line i) {
    float x1 = a.x;
    float x2 = b.x;
    float x3 = i.a.x;
    float x4 = i.b.x;

    float y1 = a.y;
    float y2 = b.y;
    float y3 = i.a.y;
    float y4 = i.b.y;

    float numeratorX = (x1*y2 - y1*x2)*(x3 - x4)-(x1 - x2)*(x3*y4 - y3*x4);
    float numeratorY = (x1*y2 - y1*x2)*(y3 - y4)-(y1 - y2)*(x3*y4 - y3*x4);
    float denumerator = (x1 - x2)*(y3 - y4) - (y1 - y2) * (x3 - x4);

    float px = numeratorX/denumerator;
    float py = numeratorY/denumerator;
    return new Point(px, py);
  }
  
  void set(float angle, float driftX, float driftY){
    a = new PVector(cos(angle) * -width + driftX, sin(angle) * -width + driftY);
    b = new PVector(cos(angle) * width + driftX, sin(angle) * width + driftY);
    slope = (a.x - b.x)/(a.y - b.y);
  }
  
}

class Point {
  float x;
  float y;
  Point(float x, float y) {
    this.x = x;
    this.y = y;
  }

  void draw() {
    noStroke();
    fill(255);
    ellipse(x, y, 5, 5);
    text("(" + floor(x * 10)/10f + ", " + floor(y*10)/10f + ")", x, y + 20);
  }
}

[ddownn]

When I draw the arrow heads, instead of giving them a fixed length like 50 in my example, I want to calculate PVectors where the lines would intersect the yellow line at the given angle of PI/6, highlighted by the light blue circles in this picture.

I’m going to update my second example code so it draws the tangent line.

Does that make sense?

[humayung]

@ddownn

When I draw the arrow heads, instead of giving them a fixed length like 50 in my example, I want to calculate PVectors where the lines would intersect the yellow line at the given angle of PI/6, highlighted by the light blue circles in this picture.

here you go

Line tail1;
Line tail2;
Line line;
float tailWide = PI/6 * 2; // Angle between tails
float arrowRotation = radians(0); // arrow rotation

PVector arcPos = new PVector(0, 0);
float arcRadius = 100;
float startAngle = PI;
float endAngle = TWO_PI;
float trimAngle = startAngle * 0.95;
void setup() {
  size(640, 360);
  noFill();
  tail1 = new Line();
  tail2 = new Line();
  line = new Line();
}

float h = 0;
void draw() {
  background(51);
  update();
  show();
}

void show() {
  translate(width/2, height/2);
  strokeWeight(1);
  PVector p1 = tail1.intersect(line);
  PVector p2 = tail2.intersect(line);
  stroke(255, 255, 0);
  line.draw();
  stroke(0, 255, 0);
  line(p1.x, p1.y, tail1.driftX, tail1.driftY);
  line(p2.x, p2.y, tail1.driftX, tail1.driftY);


  noFill();
  stroke(255);
  ellipse(arcPos.x, arcPos.y, arcRadius * 2, arcRadius*2);
  stroke(0, 255, 0);
  strokeWeight(2);
  arc(arcPos.x, arcPos.y, arcRadius * 2, arcRadius*2, startAngle, endAngle, PIE);
}

void update() {
  startAngle = (startAngle + 0.01) % TWO_PI;
  trimAngle = startAngle * 0.95;
  line.setAngle(trimAngle);

  tail1.set(arrowRotation - tailWide/2f + startAngle - HALF_PI, arcPos.x + cos(startAngle) * arcRadius, sin(startAngle) * arcRadius);
  tail2.set(arrowRotation + tailWide/2f + startAngle - HALF_PI, arcPos.x + cos(startAngle) * arcRadius, sin(startAngle) * arcRadius);
}

float arrowAngle =0;
void mouseWheel(MouseEvent e) {
  arrowAngle += e.getCount() * 0.05;
}


class Line {
  PVector a;
  PVector b;
  float driftX;
  float driftY;
  float slope;

  void draw() {
    line(a.x, a.y, b.x, b.y);
  }

  PVector intersect(Line i) {
    float x1 = a.x;
    float x2 = b.x;
    float x3 = i.a.x;
    float x4 = i.b.x;

    float y1 = a.y;
    float y2 = b.y;
    float y3 = i.a.y;
    float y4 = i.b.y;

    float numeratorX = (x1*y2 - y1*x2)*(x3 - x4)-(x1 - x2)*(x3*y4 - y3*x4);
    float numeratorY = (x1*y2 - y1*x2)*(y3 - y4)-(y1 - y2)*(x3*y4 - y3*x4);
    float denumerator = (x1 - x2)*(y3 - y4) - (y1 - y2) * (x3 - x4);

    float px = numeratorX/denumerator;
    float py = numeratorY/denumerator;
    return new PVector(px, py);
  }

  void set(float angle, float driftX, float driftY) {
    a = new PVector(cos(angle) * -width + driftX, sin(angle) * -width + driftY);
    b = new PVector(cos(angle) * width + driftX, sin(angle) * width + driftY);
    slope = (a.x - b.x)/(a.y - b.y);
    this.driftX = driftX;
    this.driftY = driftY;
  }

  void setAngle(float angle) {
    a = new PVector(cos(angle) * -width + driftX, sin(angle) * -width + driftY);
    b = new PVector(cos(angle) * width + driftX, sin(angle) * width + driftY);
    slope = (a.x - b.x)/(a.y - b.y);
  }
}

edit:
I just realized this part of creating a line is less elegant,

a = new PVector(cos(angle) * -width + driftX, sin(angle) * -width + driftY);
b = new PVector(cos(angle) * width + driftX, sin(angle) * width + driftY);

x = cos(a) * r
y = sin(a) * r
i could be simplify to this

 a = new PVector(-width + driftX, tan(angle) * -width + driftY);
 b = new PVector(width  + driftY, tan(angle) * width + driftY);

*y = tan(a)x + c

[ddownn]

Thanks, I’ll see if I can digest this

[ddownn]

@humayung

do you mean the point intersection between two line

Okay, still working on this. I like how well your solution works with the intersection test, but actually I was hoping for something a lot more basic and it seems like I found the answer in this Stack Exchange question.

I tried to really simplify the code to highlight the main goal which is how to calculate what is now called ”B2” in this new example, by modifying the variables ”b” and ”angle”. Then the arrow head can simply be drawn from ”C” to ”B2”.

x = Sin(a) / (Sin(135-a) / y)

Changing the value of angle works fine as long as "b" is 45º, but I’m still having a bit of trouble making it work when I change the value of "b" to something else. I think it is because 135º needs to change when "a" is no longer 45º, but so far I’m still muddling through it.

PVector B, C, A, B2, tanEnd;
float r, b, c, a, opp, adj, hyp, x, angle;
void setup() {
  size(400, 600);
  r = 150;
  c = radians(90);
  b = radians(-45);
  a = radians(180)-(b+c);

  angle = radians(30);
  
  opp = r;
  adj = opp*tan(b);
  hyp = opp/cos(b);   

  B = new PVector(width/2, height/2);
  C = new PVector(B.x+cos(0)*opp, B.y+sin(0)*opp);
  A = new PVector(B.x+cos(b)*hyp, B.y+sin(b)*hyp);

  x = sin(angle)/(sin(radians(135)-angle)/opp);
  B2 = new PVector(A.x+cos(radians(135))*x, A.y+sin(radians(135))*x);

  tanEnd = new PVector(C.x+cos(-HALF_PI)*opp, C.y+sin(-HALF_PI)*opp);
}

void draw() {
  background(127);
  ellipseMode(RADIUS);
  drawBaseFigure();

  strokeWeight(4);
  stroke(200, 0, 0);
  line(A.x, A.y, B2.x, B2.y);
  line(B2.x, B2.y, C.x, C.y);
}
void drawBaseFigure() {
  //drawCircle();
  drawReferenceAngle();
  drawOpposite();
  drawAdjacent();
  drawHypotenuse();
  //drawTangent();
}
void drawCircle() {
  strokeWeight(10);
  stroke(0);
  noFill();
  ellipse(B.x, B.y, opp, opp);
}
void drawOpposite() {
  strokeWeight(10);
  stroke(0);
  line(B.x, B.y, C.x, C.y);
}
void drawAdjacent() {
  strokeWeight(10);
  stroke(0);
  line(C.x, C.y, A.x, A.y);
}
void drawHypotenuse() {
  strokeWeight(10);
  stroke(0);
  line(B.x, B.y, A.x, A.y);
}
void drawTangent() {
  strokeWeight(1);
  stroke(175);
  line(C.x, C.y, tanEnd.x, tanEnd.y);
}
void drawReferenceAngle() {
  strokeWeight(10);
  stroke(255);
  pushMatrix();
  translate(C.x, C.y);
  rotate(-c-angle);
  line(0, 0, 200, 0);
  popMatrix();
}

[ddownn]

This is really infuriating. Now it seems like I’m getting closer, but at this point I feel like I’m just trying to open a lock by trying every possible combination of numbers.

Is it even possible to change the value of the angle b and have the point “b2” stay on the line?

PVector B, C, A, B2, tanEnd;
float r, b, c, a, opp, adj, hyp, x, b2, c2, a2, value;
void setup() {
  size(400, 600);
  r = 100;
  c = radians(90);
  b = radians(45); // use -b to make triangle "upright"
  a = radians(180)-(b+c);

  c2 = radians(45);
  a2 = a;
  b2 = radians(180)-(c2+a2);

  value = a+b2;
  //value = radians(135);

  opp = r;
  adj = opp*tan(b);
  hyp = opp/cos(b);

  B = new PVector(width/2, height/2);
  C = new PVector(B.x+cos(0)*opp, B.y+sin(0)*opp);
  A = new PVector(B.x+cos(-b)*hyp, B.y+sin(-b)*hyp);

  x = sin(a2)/(sin(value-a2)/opp);
  B2 = new PVector(A.x+cos(value)*x, A.y+sin(value)*x);

  tanEnd = new PVector(C.x+cos(-HALF_PI)*opp, C.y+sin(-HALF_PI)*opp);

  println("Press [j] & [l] to change angle c2.");
  println("Press [i] & [k] to change angle b.");
}
void draw() {
  background(127);
  ellipseMode(RADIUS);
  drawBaseFigure();

  strokeWeight(4);
  stroke(200, 0, 0);
  line(A.x, A.y, B2.x, B2.y);
  line(B2.x, B2.y, C.x, C.y);
  noFill();
  strokeWeight(2);
  stroke(175);
  ellipse(B2.x, B2.y, 10, 10);
}
void keyPressed() {
  if ( key == 'l' || key == 'L' ) c2-=radians(5);
  if ( key == 'j' || key == 'J' ) c2+=radians(5);
  if ( key == 'i' || key == 'I' ) b+=radians(5);
  if ( key == 'k' || key == 'K' ) b-=radians(5);
  updateFigure();
}
void updateFigure() {
  a = radians(180)-(b+c);
  a2 = a;
  b2 = radians(180)-(c2+a2);
  value = a+b2;
  adj = opp*tan(b);
  hyp = opp/cos(b);  
  A = new PVector(B.x+cos(-b)*hyp, B.y+sin(-b)*hyp);
  x = sin(a2)/(sin(value-a2)/opp);
  B2 = new PVector(A.x+cos(value)*x, A.y+sin(value)*x);
}
void drawBaseFigure() {
  //drawCircle();
  drawReferenceAngle();
  drawOpposite();
  drawAdjacent();
  drawHypotenuse();
  //drawTangent();
  showValues();
}
void drawCircle() {
  strokeWeight(10);
  stroke(0);
  noFill();
  ellipse(B.x, B.y, opp, opp);
}
void drawOpposite() {
  strokeWeight(10);
  stroke(0);
  line(B.x, B.y, C.x, C.y);
}
void drawAdjacent() {
  strokeWeight(10);
  stroke(0);
  line(C.x, C.y, A.x, A.y);
}
void drawHypotenuse() {
  strokeWeight(10);
  stroke(0);
  line(B.x, B.y, A.x, A.y);
}
void drawTangent() {
  strokeWeight(1);
  stroke(150);
  line(C.x, C.y, tanEnd.x, tanEnd.y);
}
void drawReferenceAngle() {
  strokeWeight(5);
  stroke(255);
  pushMatrix();
  translate(C.x, C.y);
  rotate(-c-c2);
  line(0, 0, 200, 0);
  popMatrix();
}
void showValues() {
  float textSz = 17;
  textSize(textSz);
  textAlign(RIGHT);
  String[] s = { 
    "c = " + nfs(degrees(c), 3, 1) + "°", 
    "b = " + nfs(degrees(b), 3, 1) + "°", 
    "a = " + nfs(degrees(a), 3, 1) + "°", 
    "c2 = " + nfs(degrees(c2), 3, 1) + "°", 
    "b2 = " + nfs(degrees(b2), 3, 1) + "°", 
    "a2 = " + nfs(degrees(a2), 3, 1) + "°"
  };
  float strWidth = 0;
  int widestStr = 0;
  for (int i = 0; i < s.length; i++) {
    if (textWidth(s[i]) > strWidth) {
      strWidth = textWidth(s[i]);
      widestStr = i;
    }
  }
  for (int i = 0; i < s.length; i++) {
    text( s[i], 5+textWidth(s[widestStr]), textSz+(i*textSz) );
  }
}

[ddownn]

From an answer to my Stack Exchange question I got this, which seems to work fairly well. But when I change the angle “c2” it is drawing the line at angle c2 CCW from BC instead of CW from AB and I’m not sure why.

PVector A, B, C, B2;
float r, opp, adj, hyp, a, b, c, a2, b2, c2, x;
void setup() {
   size(400, 600);
   
   r = 150;
   
   b = radians(20);
   c = radians(90);
   a = radians(180)-(b+c);
   
   c2 = radians(60);
   
   opp = r;
   adj = opp*tan(b);
   hyp = opp/cos(b);
   
   B = new PVector(width-75, 75);
   C = new PVector(B.x+cos(c)*opp, B.y+sin(c)*opp);
   A = new PVector(B.x+cos(c+b)*hyp, B.y+sin(c+b)*hyp);
   
   x = adj*sin(a)/sin(a-c-c2);
   
   B2 = new PVector(C.x+cos(c-c2)*x, C.y+sin(c-c2)*x);
   
   println("Press [j] & [l] to change angle c2.");
   println("Press [i] & [k] to change angle b.");
}

void draw() {
   background(127);
   
   line(B.x, B.y, C.x, C.y);
   line(C.x, C.y, A.x, A.y);
   line(B.x, B.y, A.x, A.y);
   
   line(C.x, C.y, B2.x, B2.y);
   
   showValues();
}
void keyPressed() {
   if ( key == 'l' || key == 'L' ) c2-=radians(1);
   if ( key == 'j' || key == 'J' ) c2+=radians(1);
   if ( key == 'i' || key == 'I' ) b+=radians(1);
   if ( key == 'k' || key == 'K' ) b-=radians(1);
   updateFigure();
}
void updateFigure() {
// this is the set of initializers from setup()
// any variables not affected by changes to "b" or "c2" are commented out
   //r = 150;
   //b = radians(20);
   //c = radians(90);
   a = radians(180)-(b+c);
   //c2 = radians(60);
   //opp = r;
   adj = opp*tan(b);
   hyp = opp/cos(b);
   //B = new PVector(width-75, 75);
   //C = new PVector(B.x+cos(c)*opp, B.y+sin(c)*opp);
   A = new PVector(B.x+cos(c+b)*hyp, B.y+sin(c+b)*hyp);
   x = adj*sin(a)/sin(a-c-c2);
   B2.set(C.x+cos(c-c2)*x, C.y+sin(c-c2)*x);
}
void showValues() {
   float textSz = 17;
   textSize(textSz);
   textAlign(RIGHT);
   String[] s = { 
      "c = " + nfs(degrees(c), 3, 1) + "°", 
      "b = " + nfs(degrees(b), 3, 1) + "°", 
      "a = " + nfs(degrees(a), 3, 1) + "°", 
      "c2 = " + nfs(degrees(c2), 3, 1) + "°", 
      "b2 = " + nfs(degrees(b2), 3, 1) + "°", 
      "a2 = " + nfs(degrees(a2), 3, 1) + "°"
   };
   float strWidth = 0;
   int widestStr = 0;
   for (int i = 0; i < s.length; i++) {
      if (textWidth(s[i]) > strWidth) {
         strWidth = textWidth(s[i]);
         widestStr = i;
      }
   }
   for (int i = 0; i < s.length; i++) {
      text( s[i], 5+textWidth(s[widestStr]), textSz+(i*textSz) );
   }
}