How to cube a sine/cosine function in processing

Processing Coding Questions
22

Very cool!

For TRIANGLE_FAN, that is producing a lot of little shapes. For one shape, also try:

# this is pseudocode:
beginShape
  vertex(center)
  for (0 <= 360 stepped)
    compute edgepoint
    vertex(edgepoint)
endShape

So there is only one vertex call in the loop, and the first /last point created by the loop will be the same.

1 Like
23

That worked!

  s = createShape();
  s.beginShape(TRIANGLE_FAN);
  s.vertex (0, 0, 0);
  for (int t = 1; t<steps; t++) 
    {
    float angle = t*(TAU)/steps;  
    // compute
    s.vertex(x, y, z);
    }
  s.endShape();
  shape(s, 0, 0);

Thank you.

1 Like
24

@trikaphundo
Why does it compute it like this?

Why not just like people might by using repeated multiplication.

25

Hello @Adi,

Using repeated multiplication only works for whole positive numbers (1, 2, 3, 4,…).

Using the definition with exp and log allows to use any real numbers so raising 5 to the power of -8,4 becomes possible.

1 Like
26

Hello,

My exploration of this… sharing.

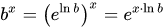
image

Using Processing functions and Java Math class and comparing results:

Code < Expand this to see code. 
// Exponential Powers Exploration
// v1.0.0
// GLV 2020-MM-DD

//https://en.wikipedia.org/wiki/Exponentiation#Powers_via_logarithms

float b = 2.0;
float x = 3.5;  

//Processing functions

float c;

c = exp(x*log(b));
println(c);

c = pow(b, x);
println(c);

println();

//Java Math class 

double d;

d = Math.exp(x*Math.log(b));
println(d);

d = Math.pow(b, x);
println(d);

Processing references:
https://processing.org/reference/log_.html
https://processing.org/reference/exp_.html
https://processing.org/reference/pow_.html

Processing down casts to a float (loss of precision):
float exp(float n)
float pow(float n, float e)
It takes a few seconds with my browser to go to line number for links above.

:)

Java references:
Java 8 Math class
Source code for pow() There may be a better link to source.

:)

3 Likes
27

Thanks for the answers. :smiley:

2 Likes